A tundra orbit is a special type of orbit meant to provide long periods of coverage to a single region at upper latitudes. Conceptually, it is somewhere between a Molniya orbit and a geosynchronous orbit.
Here is how to easily insert a new satellite with a tundra orbit using the satellite Orbit Wizard:
1) Open the "Insert STK Objects" window. Select "Satellite" as the object and "Orbit Wizard" as the method.
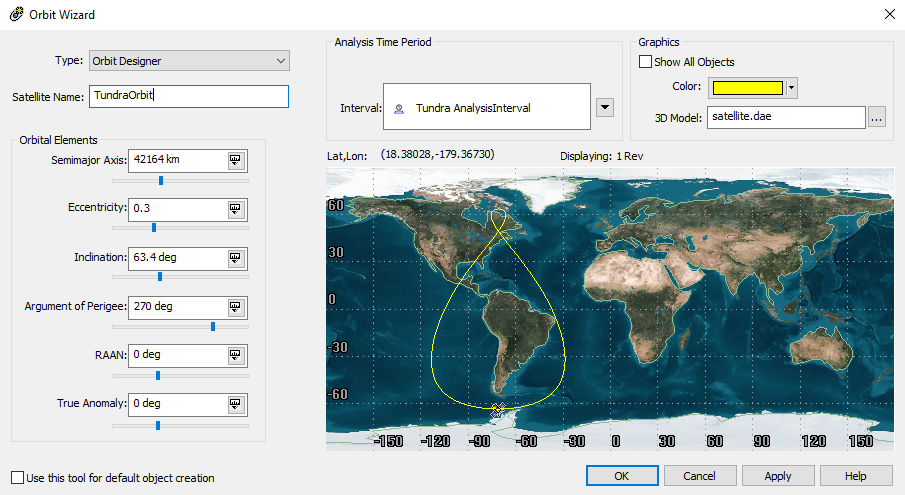
2) In the Orbit Wizard window (shown below), change Type to "Orbit Designer." Then change the following orbital elements:
Semimajor Axis:
42164 km, for a one day period
Eccentricity:
~0.2 to ~0.3, to achieve a longer dwell time in a hemisphere
Inclination:
63.4 deg, to keep the motion of Argument of Perigee due to the
Earth's J2 effect nearly constant
Argument of Perigee:
270 or 90 deg, for the northern hemisphere or southern hemisphere, respectively
RAAN: specify your own value; this moves the orbit left (west) or right (east) on the 2D projection
True Anomaly: specify your own value; changes the satellite location within the orbit at the start time
Some elements you might want to maintain in this orbit are:
-Argument of Perigee
-Eccentricity
-Orbit Period
-Inclination
-Geodetic longitude of subsatellite point at apogee
One way to do this is with the Autosequence feature in STK's
Astrogator capability. First, target the desired longitude at apogee for the initial state. The targeter solves for the right RAAN constrained by the longitude:

Construct two Autosequences. The first one is a 4x4 targeter that will retain the eccentricity, argument of perigee, orbit period, and the longitude at apogee.
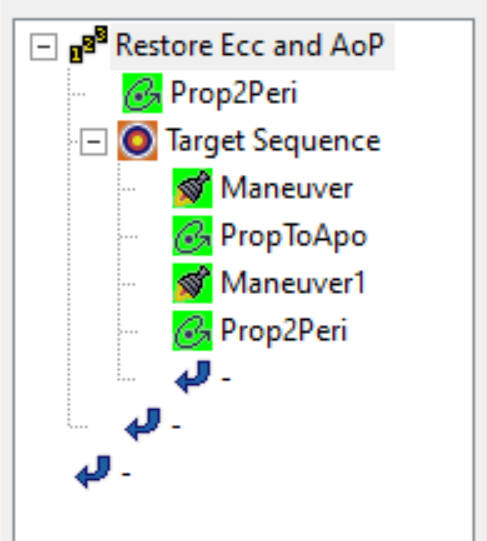
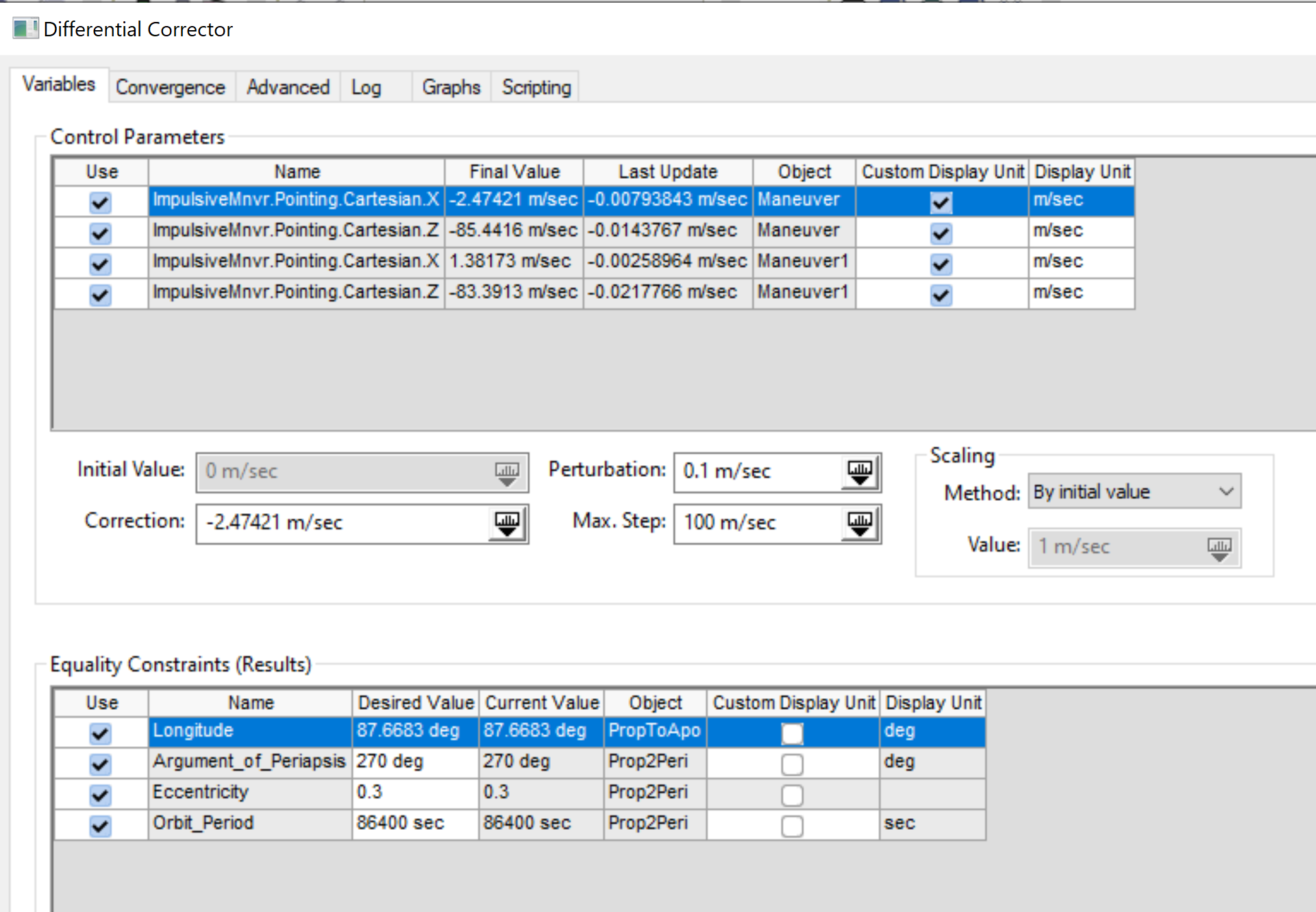
The spacecraft propagates to perigee and fires an impulsive burn in the velocity and conormal directions, and it does this at apogee as well. The longitude is constrained at apogee, but the rest must be constrained at perigee. The differential corrector has to account for both burns, especially in the velocity direction, so it must be constrained at the very end of the sequence. For example, if the eccentricity were constrained at apogee instead, then the second maneuver would undo the correction and have a different eccentricity by the end.
The second Autosequence is a 3x3 targeter that corrects the inclination while maintaining the eccentricity and altitude at apogee.
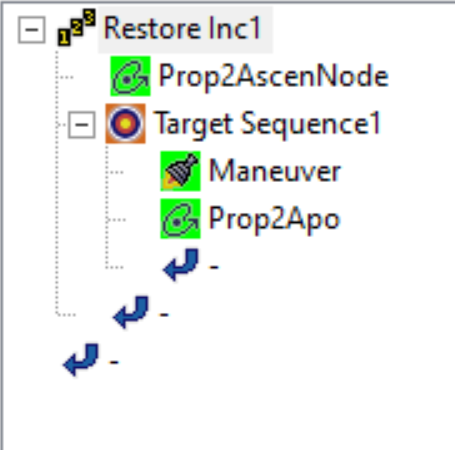
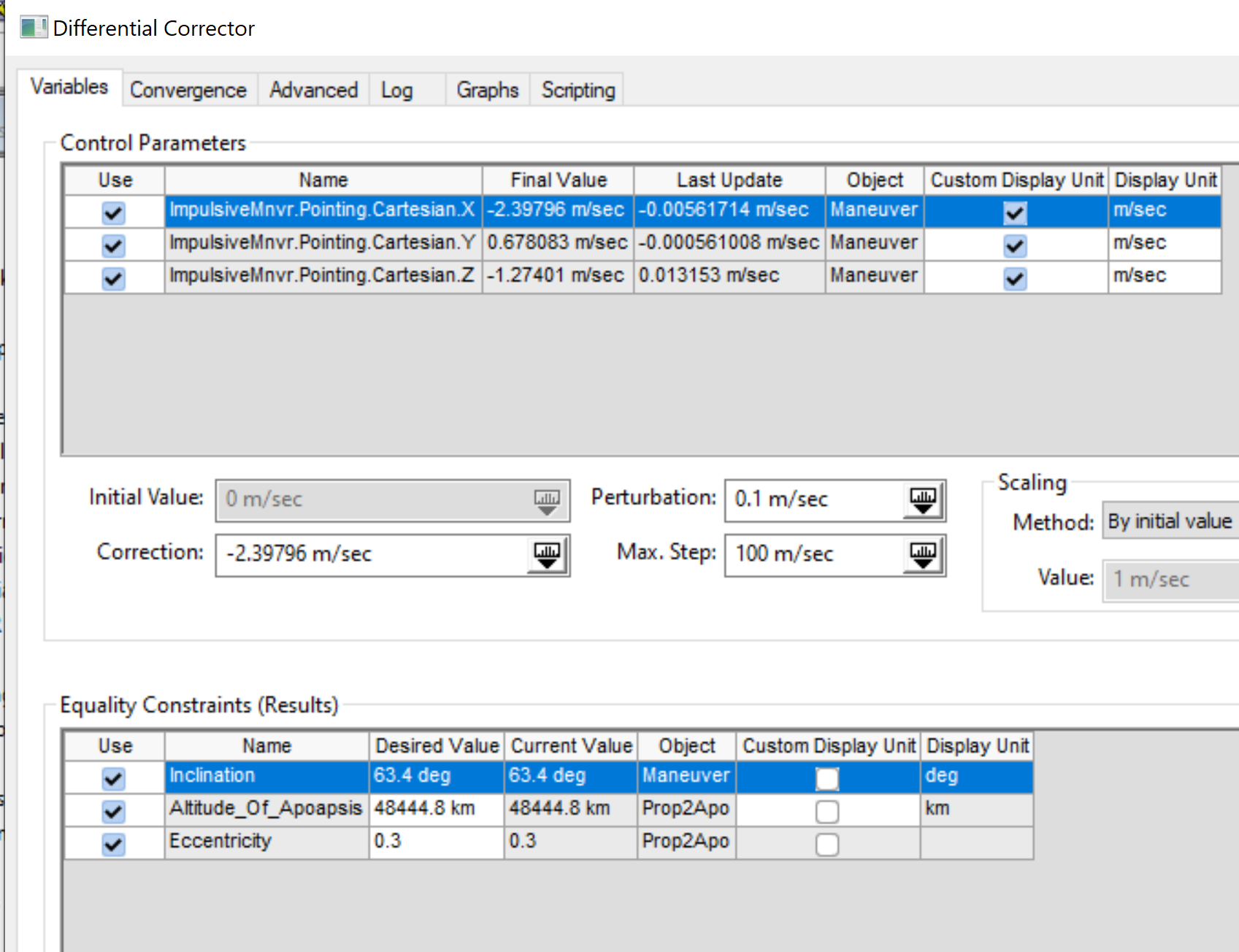
Burning out of plane will alter the eccentricity, and attempting to alter the eccentricity at a node will change a lot too. Therefore, link the altitude, inclination, and eccentricity, to restore the inclination without disturbing the trajectory.
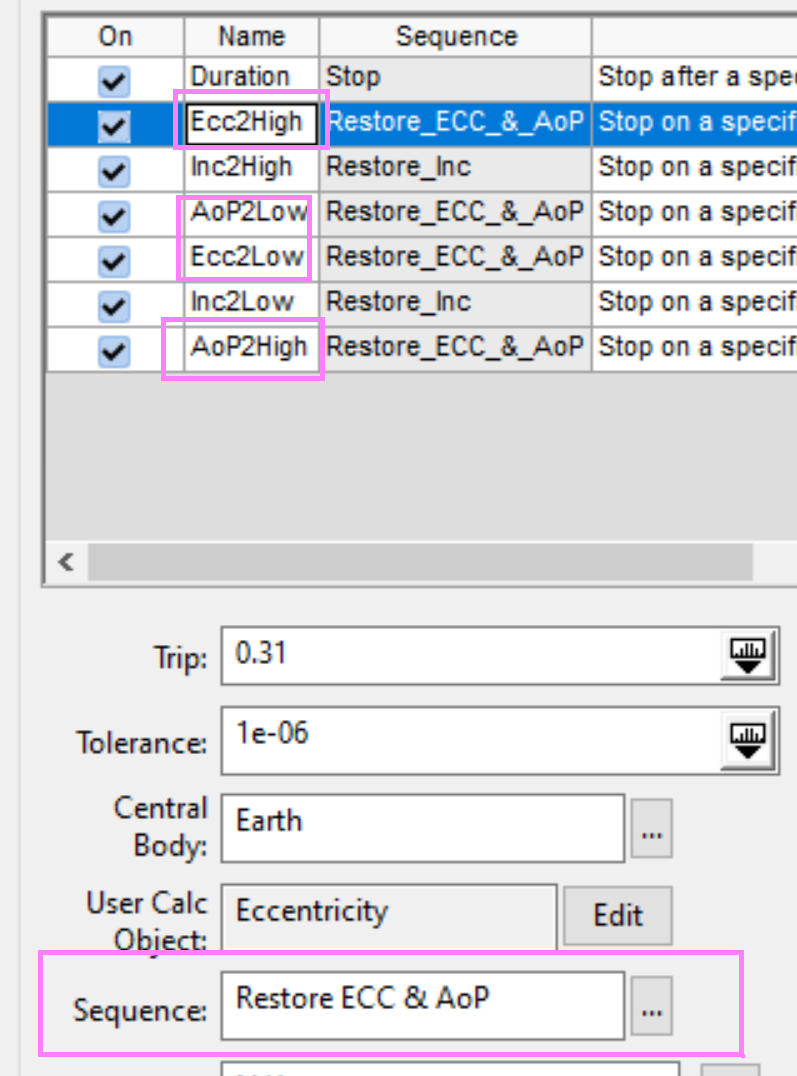
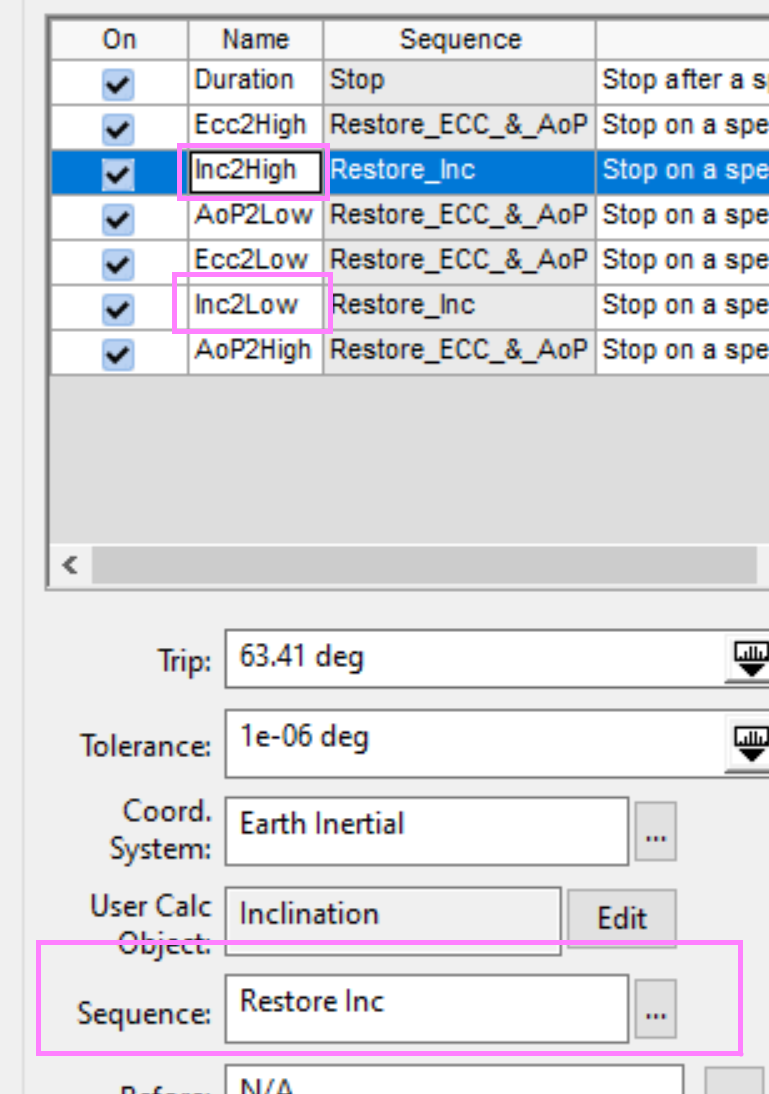
You need to apply seven stopping conditions to the propagate segment. One is for the duration that this spacecraft will be analyzed for, and then three each for the upper and lower thresholds of argument of perigee, eccentricity, and inclination that will trigger the autosequences.
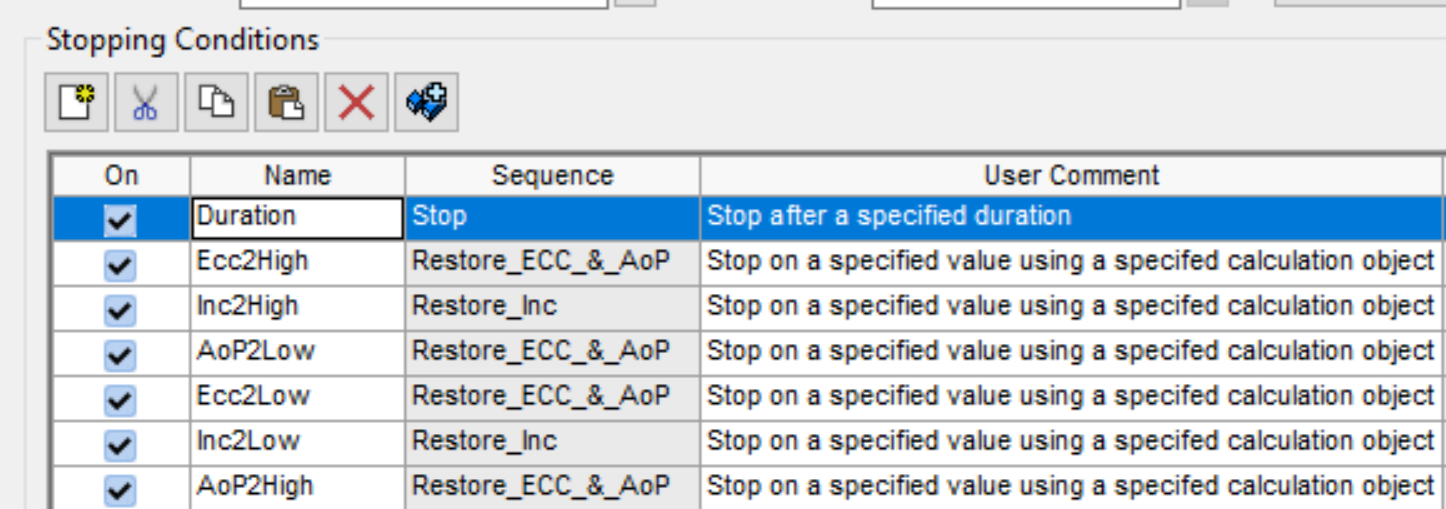
The bounds for each are the following:
-Inclination = [63.39,63.41]
-Eccentricity = [0.29,0.31]
-Argument of Perigee = [269.9,270.1]
The eccentricity and argument of perigee stopping conditions will combine to trigger a sequence, and the inclination stopping condition will trigger the second one. The duration for this example is set to 200 days, to get a good view of the behavior.
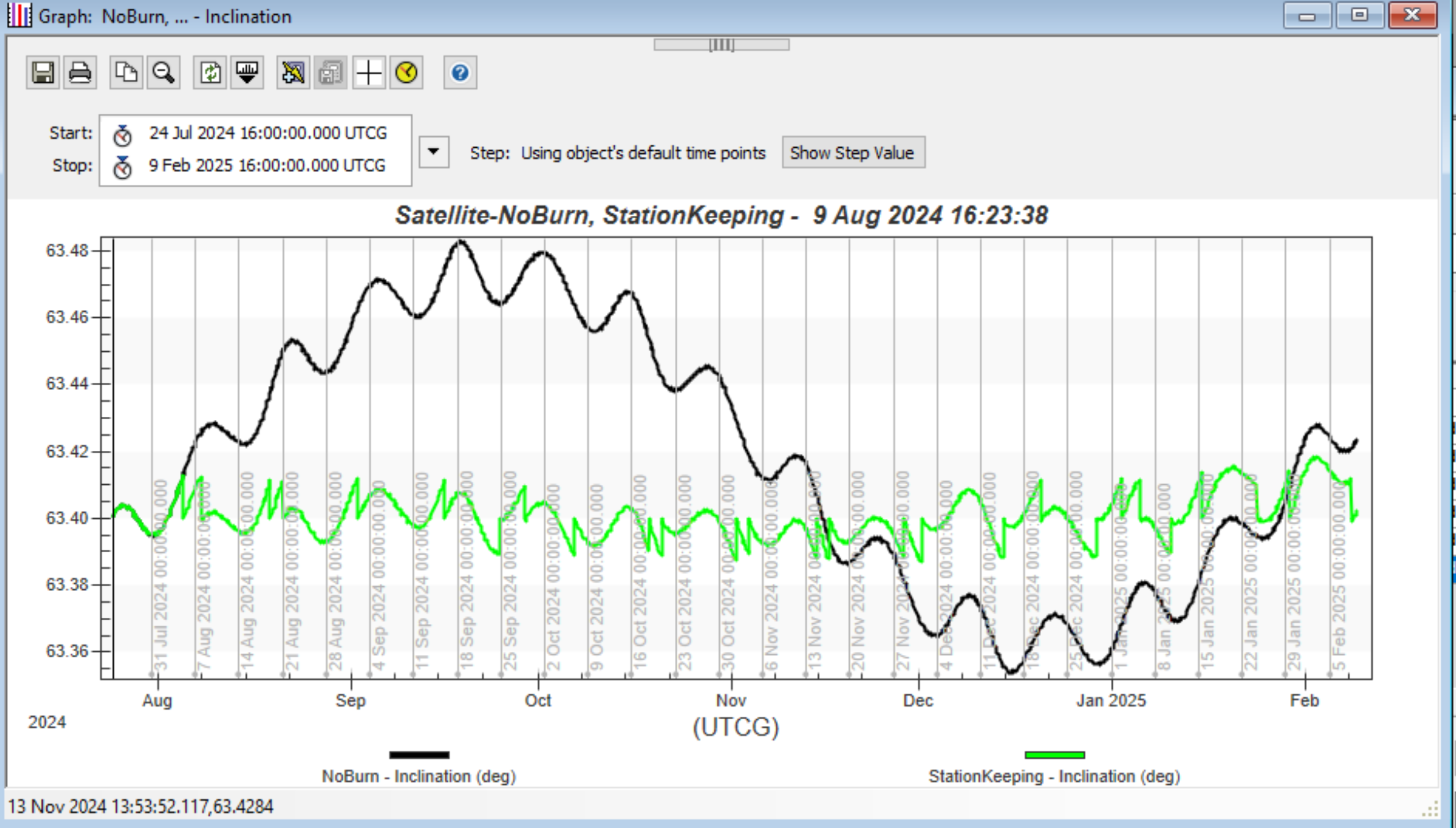
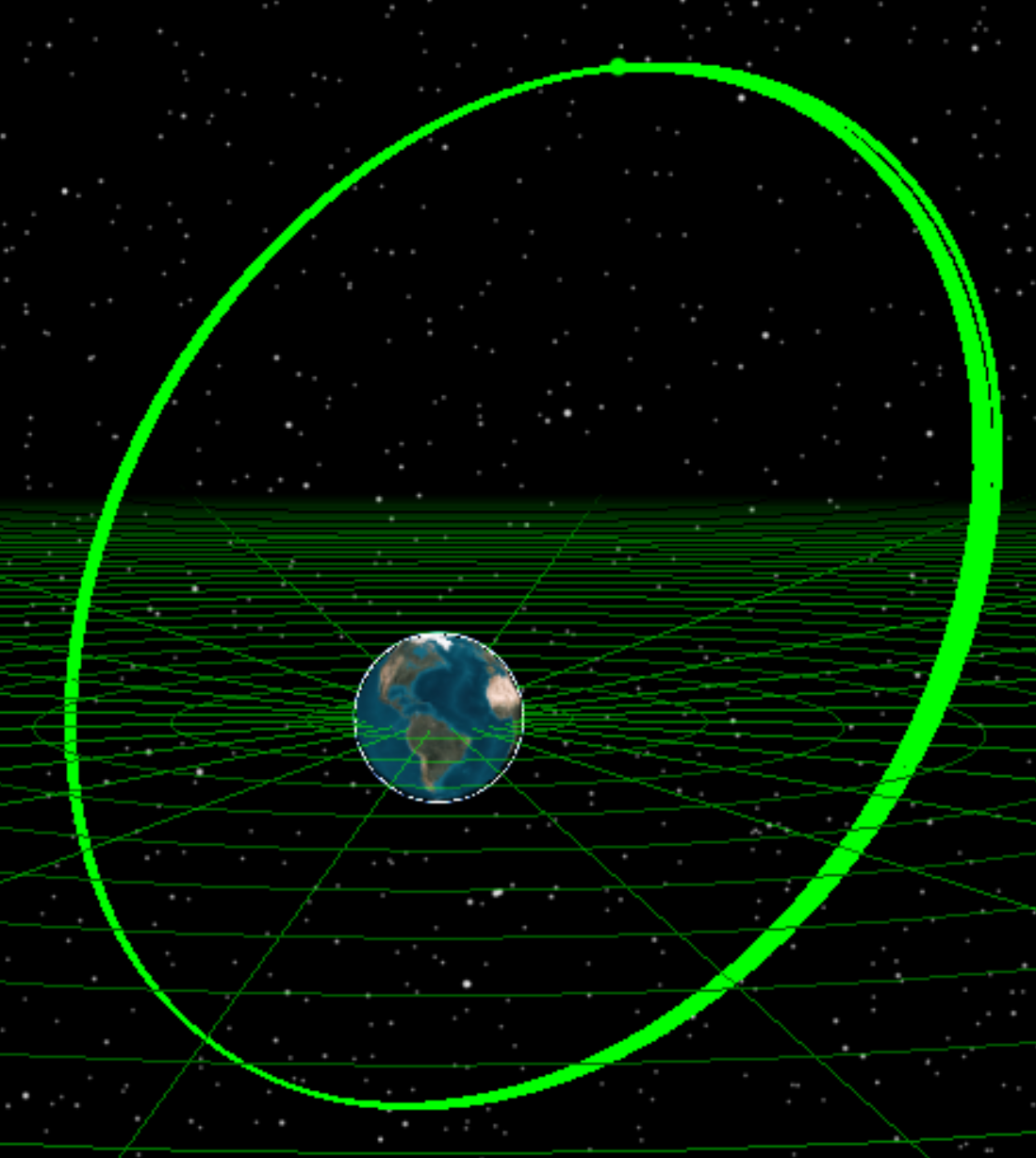
After running the MCS, you can look at how the orbit was maintained. This green orbit is your station-keeping satellite trajectory.
Analyzing the argument of perigee, you can see that the associated autosequence is triggered about twice a month. The black line is a control satellite, for reference, that has not undergone any maneuvers. The spikes indicate the argument of perigee increasing slightly during the first maneuver before being fully restored by the second maneuver.
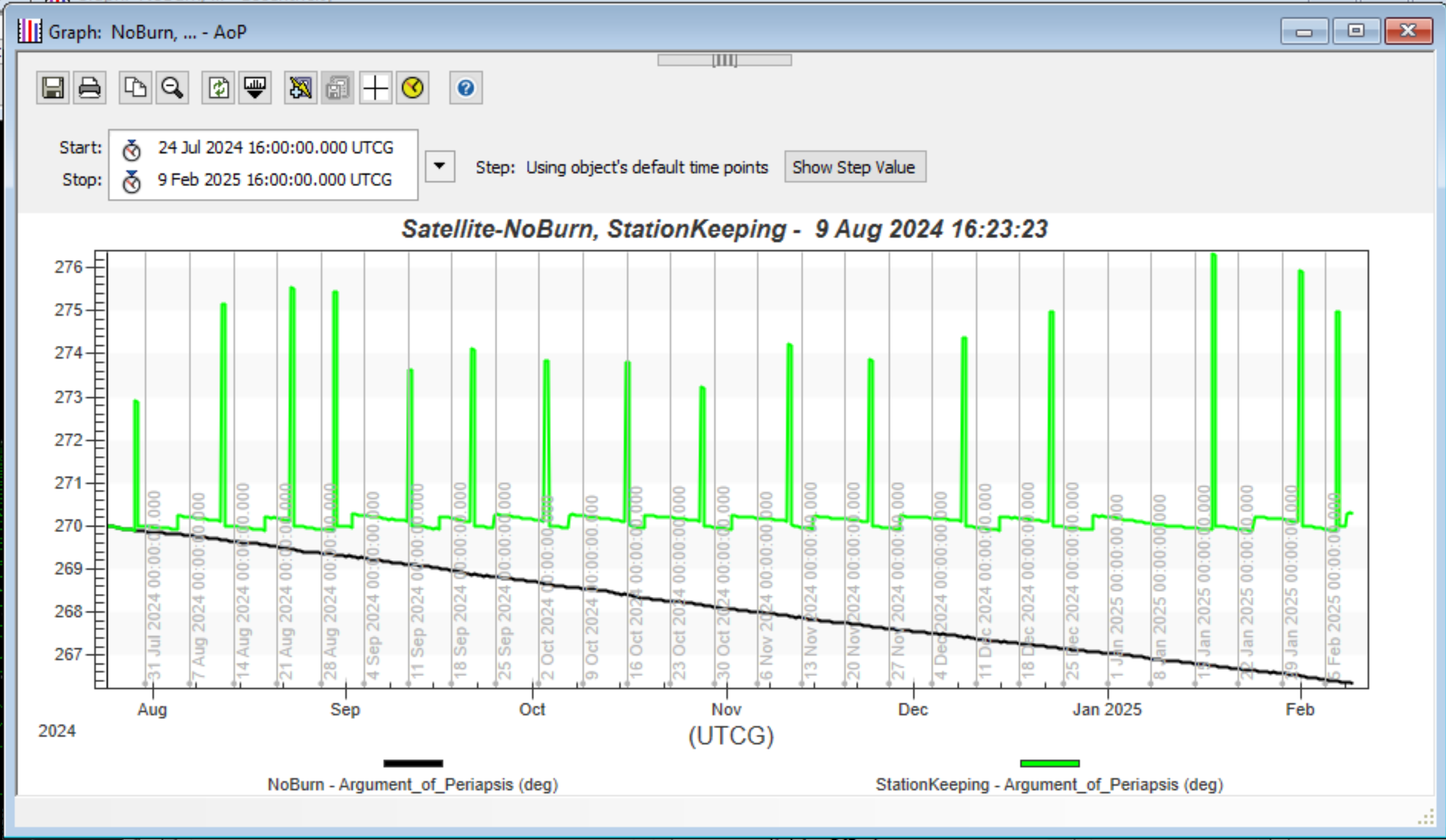
You can see that if you do no station-keeping, the satellite's argument of perigee would decrease.
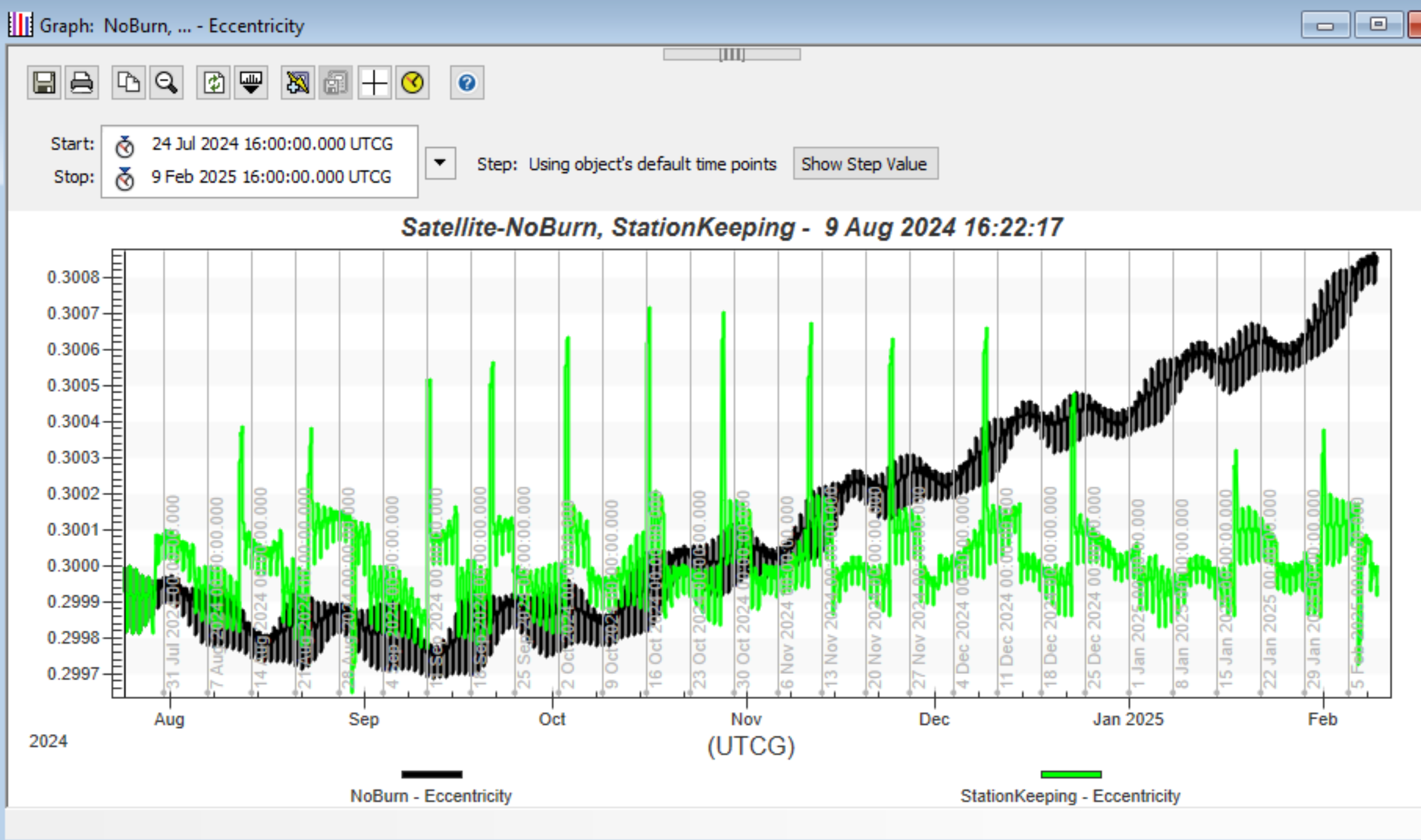
Analyzing the eccentricity, you can see that without station-keeping, the eccentricity would increase.
Analyzing the inclination, you can see the larger oscillations without the station-keeping.